随机非线性薛定谔方程是偏微分方程领域最近几十年最受关注和最有影响的研究方向之一。上海科技大学数学科学研究所助理教授岳海天与合作者在该方向取得了重要进展。相关成果发表在11月17日出版的《数学新进展》(Inventiones Mathematicae)上。该期刊是世界四大顶尖数学期刊之一。
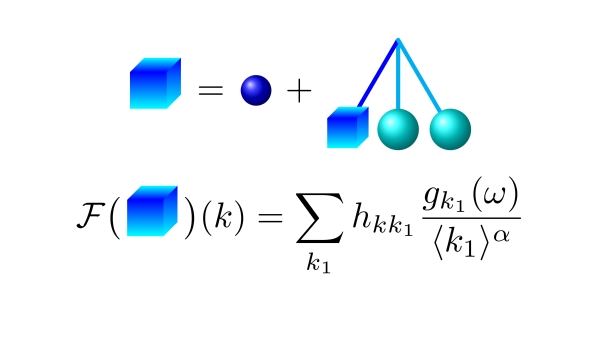
以薛定谔方程为代表的非线性色散偏微分方程是一种描述广泛存在于自然界中的色散现象的偏微分方程,其应用领域包括量子物理、光学、凝聚态物理、水波方程等。随机初值方法是数学上理解常规初值在非线性偏微分方程下演化问题的经典方法,而低正则性的随机初值问题则是统计力学中吉布斯测度不变性的数学验证中的一个核心问题。岳海天与美国南加州大学教授邓煜和马萨诸塞大学阿默斯特分校教授Andrea Nahmod创建了随机张量理论(random tensor theory),解决了一类非线性薛定谔方程概率次临界的低正则性随机初值下的短时间适定性问题,并且通过随机张量提供了对不同频率随机演化相互作用的精确描述。该理论是菲尔兹奖得主辛康·布尔甘自1996年以来在这个研究方向最重要的进展之一,它大力地推进了人们对随机初值在非线性色散方程下演化结构的理解。
岳海天的文章是最近两年上科大数学科学研究所在《数学新进展》上发表的第二篇论文。数学所创始所长、特聘教授陈秀雄表示:“岳海天教授的成果令人鼓舞,也让我对实现数学所的愿景更有信心。”
论文链接 https://link.springer.com/article/10.1007%2Fs00222-021-01084-8